Introduction to Policy Gradient

Problem Setup

For simplicity, let us first consider a one-step decision-making process (also known as a contextual bandit).

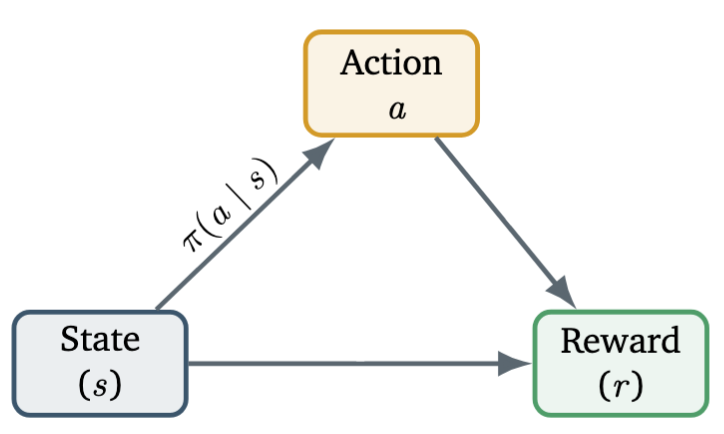
Let $s\in \mathcal{S}$ be the state vector of the environment, describing the current situation or configuration the agent observes (for example, the position of a robot, or the market condition in trading). Let $a\in \mathcal{A}$ be the action taken by the agent — a decision or move that affects the environment (e.g., moving left/right, buying/selling). The reward function, denoted by $r(a,s)$, assigns a numerical score to each action–state pair, indicating how desirable the action is when taken in that state.

The agent’s behavior is characterized by a policy, represented as a conditional probability distribution $\pi (a\mid s),$ which specifies the probability of selecting each possible action $a$ given the current state $s$.

The objective is to learn an optimal policy ${\pi }^{\ast }$ that maximizes the expected reward under the environment’s state distribution. Formally, we define the performance of a policy $\pi$ as

$$R(\pi )={\mathbb{E}}_{s\sim p_0}{\mathbb{E}}_{a\sim \pi (\cdot \mid s)}[r(a,s)],$$

which can equivalently be written as a joint expectation:

$$R(\pi )=\sum _{s,a}{p}_{\pi }(s,a)r(a,s),$$

where $p_0(s)$ denotes the (unknown) distribution of states in the environment, and

$$p_{\pi }(s,a)=p_0(s)\pi (a\mid s)$$

is the joint distribution of states and actions induced by the policy $\pi$.

In practice, the state distribution $p_0$ is rarely known in closed form; instead, we have access to a finite set of samples $\{s^{(i)}{\}}_{i=1}^N$ drawn from $p_0$, typically obtained from interaction with the environment or an existing dataset.

Policy Gradient

In practice, the policy ${\pi }_{\theta }(a\mid s)$ is parameterized by a differentiable function. The gradient of the expected reward is:

$${\nabla }_{\theta }R({\pi }_{\theta })={\mathbb{E}}_{p_{{\pi }_{\theta }}}\left[r(a,s){\nabla }_{\theta }\log {\pi }_{\theta }(a\mid s)\right].$$

(Used the log-derivative trick: ${\nabla }_{\theta }{\pi }_{\theta }/{\pi }_{\theta }={\nabla }_{\theta }\log {\pi }_{\theta }$.)

---

Reward Baseline

For any policy ${\pi }_{\theta }$:

$${\mathbb{E}}_{a\sim {\pi }_{\theta }(\cdot |s)}[{\nabla }_{\theta }\log {\pi }_{\theta }(a\mid s)]=0.$$

Hence,

$${\nabla }_{\theta }R({\pi }_{\theta })={\mathbb{E}}_{p_{{\pi }_{\theta }}}\left[(r(a,s)-v(s)){\nabla }_{\theta }\log {\pi }_{\theta }(a\mid s)\right],$$

where $v(s)$ is any function independent of $a$.

Choosing $v(s)={\mathbb{E}}_a[r(a,s)]$ gives the advantage function:

$$A(a,s)=r(a,s)-v(s).$$

A positive $A(a,s)$ means the action performs above average.

On-Policy Estimation

Given data $\{(s_i,a_i)\}$ with $s_i\sim p_0$ and $a_i\sim {\pi }_{\theta }(\cdot |s_i)$,

$${\nabla }_{\theta }R({\pi }_{\theta })\approx \frac{1}{n}\sum _{i=1}^n{A}_i{\nabla }_{\theta }\log {\pi }_{\theta }(a_i\mid s_i),$$

with $A_i=A(a_i,s_i)$.

Gradient ascent update (REINFORCE):

$$\theta \leftarrow \theta +ϵ{\nabla }_{\theta }R({\pi }_{\theta }).$$

Intuitively:

• $A_i>0$: increase ${\pi }_{\theta }(a_i|s_i)$;
• $A_i<0$: decrease it.

---

Connection to Weighted MLE

If data $(a_i,s_i)$ are fixed, the policy gradient equals the gradient of the advantage-weighted log-likelihood:

$$\ell ({\pi }_{\theta })=\frac{1}{n}\sum _{i=1}^n{A}_i\log {\pi }_{\theta }(a_i\mid s_i).$$

Thus, policy optimization ≈ adaptive MLE with dynamic weights $A_i$.

---

Off-Policy Estimation (Importance Sampling)

If data are drawn from a behavior policy ${\pi }^{\text{data}}$:

$${\nabla }_{\theta }R({\pi }_{\theta })={\mathbb{E}}_{p_{{\pi }^{\text{data}}}}\left[\frac{{\pi }_{\theta }(a|s)}{{\pi }^{\text{data}}(a|s)}A(a,s){\nabla }_{\theta }\log {\pi }_{\theta }(a\mid s)\right].$$

Empirically,

$${\nabla }_{\theta }R({\pi }_{\theta })\approx \frac{1}{z}\sum _{i=1}^n{w}_i{A}_i{\nabla }_{\theta }\log {\pi }_{\theta }(a_i|s_i),w_i=\frac{{\pi }_{\theta }(a_i|s_i)}{{\pi }^{\text{data}}(a_i|s_i)},$$

with normalization $z={\sum }_i{w}_i$.

---

Proximal Policy Optimization (PPO)

Proximal Point Method

Starting from ${\theta }^0$, iterate:

$${\theta }^{k+1}=\arg \underset{\theta }{\max }R(\theta )-\beta D(\theta ,{\theta }^k),$$

where $D$ measures the deviation between parameters (e.g., squared distance or KL divergence).

This forms the basis for proximal methods.

---

Proximal Gradient & Preconditioning

Approximate $R(\theta )$ by its first-order Taylor expansion:

$${\theta }^{k+1}=\arg \underset{\theta }{\max }\nabla R({\theta }^k{)}^{\top }(\theta -{\theta }^k)-\beta D(\theta ,{\theta }^k).$$

If $D(\theta ,{\theta }^k)=\frac{1}{2}(\theta -{\theta }^k{)}^{\top }J({\theta }^k)(\theta -{\theta }^k)$,

then the update is:

$${\theta }^{k+1}={\theta }^k+J({\theta }^k{)}^{-1}\nabla R({\theta }^k),$$

known as preconditioned gradient descent.

---

Remark. The proximal point framework interpolates between fast-updating methods (gradient descent) and slower, more implicit schemes, depending on how the reference point ${\theta }^{\text{ref},k}$ evolves.

• ${\theta }^{\text{ref},k}={\theta }^k$: proximal gradient descent
• ${\theta }^{\text{ref},k}={\theta }^{m\lfloor k/m\rfloor }$: inner-loop updates
• EMA of past iterates → smoother, more stable updates

---

Proximal Policy Optimization (PPO)

Applying the proximal framework to policy optimization with importance sampling:

$${\theta }^{k+1}=\arg \underset{\theta }{\max }\left\{{\mathbb{E}}_{\mathcal{D}}\right[\frac{{\pi }^{\theta }(a|s)}{{\pi }^{\text{data}}(a|s)}r(a,s)]-\beta D({\pi }^{\theta }\Vert {\pi }^{{\theta }^k})\}.$$

The penalty term is usually the KL divergence:

$$D({\pi }^{\theta }\Vert {\pi }^{{\theta }^k})={\mathbb{E}}_{s\sim p_0}[\mathrm{KL}({\pi }^{\theta }(\cdot |s)\Vert {\pi }^{{\theta }^k}(\cdot |s))].$$

---

Clipping Objective

PPO further introduces a clipping function:

$${\theta }^{k+1}=\arg \underset{\theta }{\max }{\mathbb{E}}_{\mathcal{D}}\left[\mathcal{C}(w_{\theta }(a,s),r(a,s))\right]-\beta D({\pi }^{\theta }\Vert {\pi }^{{\theta }^k}),$$

where $w_{\theta }(a,s)=\frac{{\pi }^{\theta }(a|s)}{{\pi }^{\text{data}}(a|s)}$ and

$$\mathcal{C}(w,r)=\min (wr,\text{clip}(w,[1-ϵ,1+ϵ]),r).$$

Different choices of penalty $D$ and clipping function yield different stability–efficiency tradeoffs.